444等于6怎么算，444等于6的数学原理与计算方法

平方根组合解法

三个4通过平方根符号组合实现等式：√4 √4 √4 = 2 2 2 = 6。此方法依赖平方根运算将4转化为2，叠加三个2达成目标值。

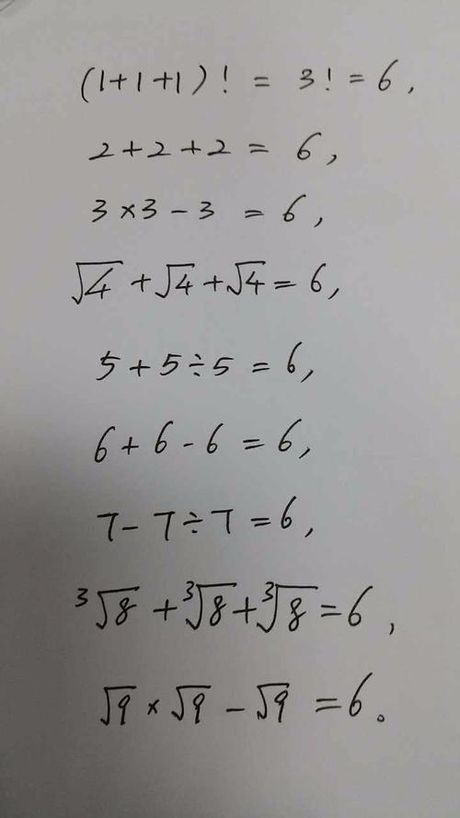
平方根符号在此处作为数学算子，满足等式成立条件。每个√4严格等于2，无近似取值。

混合运算扩展形式

除加法外，混合乘加运算同样有效：√4 × √4 √4 = (2×2) 2 = 6。此形式遵循先乘除后加减原则，√4×√4优先计算得4，再加2得6。

交换律在此类运算中成立：√4 √4 × √4 等价于原式，结果不变。

另一变体采用加减法：4 4 − √4 = 8 − 2 = 6。此解避免连续开方，直接利用整数与平方根组合。

其他数字的等效解法

• 888=6：8 8^0.5 − 8^0.5 = 8 (√8) − (√8) = 6，需重复开方
• 999=6：√9 × √9 − √9 = 3×3 − 3 = 6
• 111=6：(1 1 1)! = 3! = 3×2×1 = 6，运用阶乘运算

数位根理论的争议解释

部分观点主张数位根计算法：4 4 4=12，1 2=3，引申得出444 mod 9 = 6。此解释存在逻辑矛盾，实际444÷9=49×9 3，余数为3而非6。

数位根理论在此问题中不适用，平方根解法具数学严谨性。