定义
符号函数sgn(Signum function)是数学中用于提取实数符号的逻辑函数。定义如下:
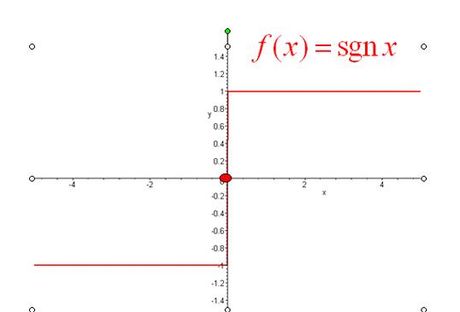
- 当 \( x > 0 \) 时,\( \text{sgn}(x) = 1 \)
- 当 \( x = 0 \) 时,\( \text{sgn}(x) = 0 \)
- 当 \( x < 0 \) 时,\( \text{sgn}(x) = -1 \)
定义域为全体实数,值域为 \( \{-1, 0, 1\} \)。该函数在\(x=0\)处存在跳跃间断点。
数学性质
等价表达式
符号函数可通过其他数学形式等价表示:
- 艾佛森括号表示:\( \text{sgn}\,x = -[x<0] [x>0] \)
- 绝对值关联:\( x = (\text{sgn}\,x) \cdot |x| \)(\(x \neq 0\) 时 \( \text{sgn}\,x = \frac{x}{|x|} \))
- 阶跃函数表示:\( \text{sgn}\,x = 2u(t) - 1 \),其中 \( u(t) \) 为单位阶跃函数
微分特性
- 与绝对值函数的关系:\( \frac{d|x|}{dx} = \text{sgn}\,x \)(\(x \neq 0\))
- 非零点导数为零,原点不可导
- 广义函数意义下:\( \frac{d\,\text{sgn}\,x}{dx} = 2\delta(x) \),其中 \( \delta(x) \) 为狄拉克δ函数
整体特性
- 奇函数性质:\( \text{sgn}(-x) = -\text{sgn}(x) \)
- 单调性:在整个定义域上不严格递增
- 可积性:在任意闭区间上Riemann可积,但不存在原函数
应用场景
数学分析
- 说明可积函数不一定存在原函数:因\(x=0\)是跳跃间断点,在任何包含原点的区间上,\(\text{sgn}(x)\)不存在原函数,此性质澄清了可积性与原函数存在性的关系
- 简化含绝对值的积分运算:通过将绝对值转化为符号函数与表达式的乘积,将积分过程简化为分段常数积分
工程与信号处理
- 控制系统:判断系统状态变量是否偏离平衡点,简化非线性系统分析
- 信号极性检测:识别音频信号的正负相位变化,应用于数字信号分类
- 分段函数建模:作为基础组件构建复杂的分段连续函数
复数推广
符号函数可扩展至复数域(\(z \in \mathbb{C} \backslash \{0\}\)):
- 基本定义:\( \text{sgn}\,z = \frac{z}{|z|} \)
- 辐角表示:\( \text{sgn}\,z = \exp(i \arg z) \)
- 原点补充定义:通常设定 \( \text{sgn}\,0 = 0 \)
另有变体 csgn 函数(Complex Sign Function):
- 当实部 \( \Re(z) > 0 \) 或(实部为零且虚部为正)时,输出 1
- 当实部 \( \Re(z) < 0 \) 或(实部为零且虚部为负)时,输出 -1
- 原点处输出 0
MATLAB实现
MATLAB 内置 sign() 函数实现符号函数功能:
- 标量输入:sign(-5) 返回 -1
- 向量/矩阵输入:sign([-5, 0, 3]) 返回 [-1, 0, 1]
- 复数处理:仅依据实部符号返回结果(如 sign(-3 4i) 返回 -1)
不可导问题处理
符号函数在原点不可导的性质可能影响数值计算:
- 平滑近似法:使用可导函数替代,如双曲正切函数 \( \tanh(kx) \) 或 Sigmoid 函数,其中 \( k \) 控制逼近陡度
- 分段条件处理:在编程实现中通过条件语句规避原点求导