函数的奇偶性是数学中一个基本且重要的概念,它描述了函数在原点或y轴上的对称性。了解如何判断一个函数的奇偶性,对于深入理解函数的性质和应用至关重要。
定义法
最基本的判断方法是定义法。如果对于函数y=f(x)的定义域内的任意一个x,都有f(-x) = -f(x),则函数f(x)是奇函数。若f(-x) = f(x),则函数f(x)是偶函数。这种方法直接根据奇偶函数的定义来判断,是最直接和常用的方法。
求和(差)法
另一种方法是求和(差)法。若f(x) - f(-x) = 2f(x),则f(x)为奇函数。若f(x) f(-x) = 2f(x),则f(x)为偶函数。这种方法通过比较f(x)和f(-x)的和或差来判断函数的奇偶性。
求商法
求商法是通过比较f(-x)和f(x)的比值来判断。若f(-x) / f(x) = -1(f(x) ≠ 0),则f(x)为奇函数。若f(-x) / f(x) = 1(f(x) ≠ 0),则f(x)为偶函数。这种方法适用于当直接比较f(x)和f(-x)较复杂时。
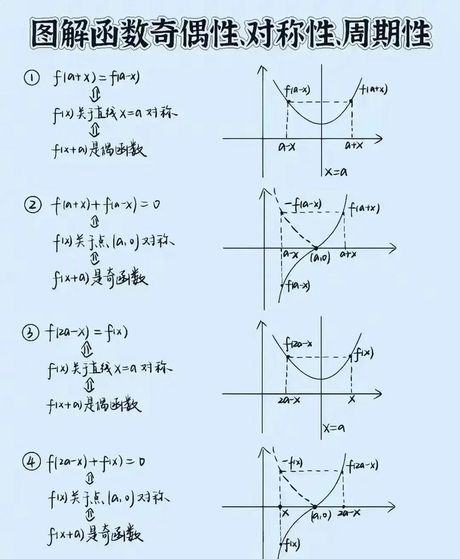
图像判断法
图像判断法是通过观察函数图像来判断奇偶性。奇函数的图像关于原点对称,而偶函数的图像关于y轴对称。这种方法直观且易于理解,但可能需要一定的图形处理技巧。
总结
判断函数的奇偶性有多种方法,包括定义法、求和(差)法、求商法和图像判断法。每种方法都有其特点和适用场景。掌握这些方法有助于深入理解函数的性质,并在解决实际问题时作出更准确的判断。