在数学的世界里,n的阶乘是一个充满神秘和趣味的概念。它代表了从1乘到$n$的所有整数的乘积,用数学符号表示为$n!$。例如,$5!$就是$5 \times 4 \times 3 \times 2 \times 1$。
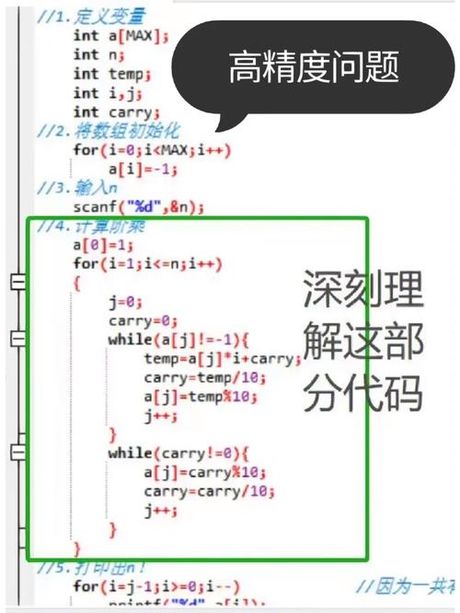
阶乘的概念在许多数学和科学领域都有应用,比如在排列组合、概率论和统计学中。它帮助我们计算在特定情况下可能发生的事件的总数。
阶乘的计算
计算阶乘的方法很简单,但结果却迅速增长。例如,$10!$等于$3628800$。当你尝试计算更大的数的阶乘时,数字会变得非常庞大,超出普通计算器的处理能力。
阶乘的用途
阶乘在数学中有着广泛的应用。在排列组合中,它帮助我们计算从$n$个不同元素中取出$r$个元素的排列数,即$P(n, r) = \frac{n!}{(n-r)!}$。在概率论中,阶乘用于计算事件的可能性,比如掷骰子得到特定数字组合的概率。
阶乘的极限
当$n$趋向于无穷大时,$n!$的增长速度是惊人的。在数学和物理学的一些理论中,我们会遇到非常大的阶乘,这时候就需要使用特殊的数学技巧来处理这些巨大的数字。
$n$的阶乘是数学中一个强大而有趣的概念,它在许多领域都有着重要的应用。了解阶乘不仅能帮助我们解决实际问题,还能让我们更深入地理解数学的魅力。