在数学的世界里,递等式计算是一种基本而强大的工具,它帮助我们理解和解决各种数学问题。简单来说,递等式计算就是通过一系列的逻辑步骤,将一个复杂的数学表达式简化为更易理解的形式。
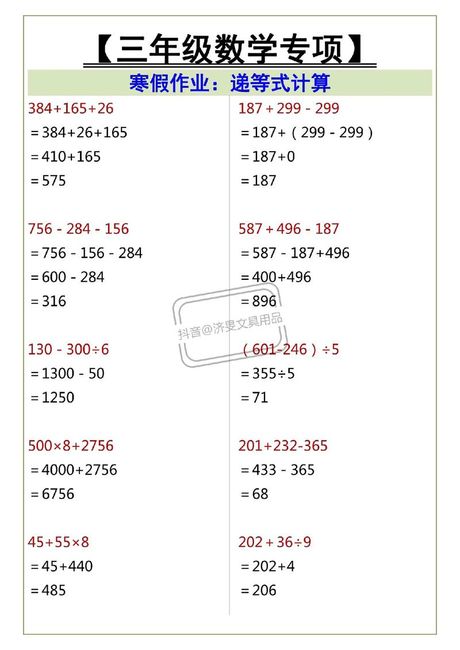
什么是递等式?
递等式,顾名思义,就是两个表达式之间通过等号连接,表示它们在数学意义上是相等的。例如,著名的勾股定理可以表示为 a^2 b^2 = c^2,其中 a、b、c 分别代表直角三角形的两个直角边和斜边。这个等式就是递等式的一个例子,它表明了直角三角形三边长度之间的关系。
递等式计算的意义
递等式计算不仅仅是一种数学技巧,它更是一种逻辑思维的艺术。通过递等式计算,我们可以:
- 简化问题:将复杂的数学问题转化为更简单、更易解决的形式。
- 发现规律:在递等式的转化过程中,我们往往能发现数学问题背后的规律和联系。
- 验证假设:通过递等式计算,我们可以验证某些数学假设或理论的真实性。
递等式计算的应用
递等式计算在数学的各个分支中都有广泛的应用。例如:
- 代数:通过递等式计算,我们可以解方程、化简代数表达式等。
- 几何:在几何学中,递等式计算帮助我们理解和证明各种几何定理。
- 微积分:在微积分中,递等式计算是理解和应用极限、导数和积分等概念的基础。
总结
递等式计算是数学中的一种基本工具,它不仅帮助我们解决数学问题,还培养了我们逻辑思维和抽象思考的能力。通过递等式计算,我们可以更深入地理解数学的本质,欣赏数学的美丽和力量。